概率论小结

基本概念

样本空间

样本空间是所有可能结果的集合，通常用符号 Ω 表示。
例如，投掷一枚骰子的样本空间为 Ω = {1, 2, 3, 4, 5, 6}。

事件

事件是样本空间的子集，通常用符号 A, B, C 等表示。
例如，投掷一枚骰子得到偶数的事件可以表示为 A = {2, 4, 6}。

概率的定义

概率是事件发生的可能性，通常用符号 P(A) 表示。
概率的定义有多种，常见的有古典概型、几何概型、条件概率等。

古典概型（等可能概型）

适用场景：当样本空间中的元素只有有限个，且每个元素出现的可能性相同。

具有以下两个条件的随机试验称为古典概型：

样本空间中的元素只有有限个；
每个元素出现的可能性相同。

设试验 E 共有 n 个可能结果，即样本空间 Ω
由 n 个样本点构成， A 为 E 的任意一个事件，且
包含 k 个样本点（也称有利于 A 的样本点数），
则事件 A 出现的概率记为 :

$$
P(A) = \frac{k}{n}
$$

古典概型中抽取问题的计算

一个盒子中三个红球和两个白球，任取两个，求取到的两个球中一个红一个白的概率。

解答

记事件 A 为取到的两个球中一个红一个白。

有利于 A 的样本点数为 $C_3^1 \times C_2^1 = 6$，这里代表从 3 个红球中选一个，从 2 个白球中选一个。

样本空间中的样本点数为 $C_5^2 = 10$，这里代表从 5 个球中选 2 个。

因此，事件 A 的概率为

$$
P(A) = \frac{6}{10} = 0.6
$$

那么如何计算这个 $C_5^2$ 呢？是按照如下阶乘公式计算的：

$$
C_5^2 = \frac{5!}{2!(5-2)!} = \frac{5 \times 4 \times 3 \times 2 \times 1}{2 \times 1 \times 3 \times 2 \times 1} = 10
$$

实际上，我们可以使用一种更简单的“约去”方法来计算组合数：

分子：从最大数开始，连续相乘，乘数的个数等于上标的数字。
分母：从 1 开始，连续相乘，直到下标的数字。

因此，$C_5^2$ 可以这样计算：

$$
C_5^2 = \frac{5 \times 4}{2 \times 1} = 10
$$

这种方法更直观，计算更快，特别是在处理大数时非常有效。

古典概型例题 1

某城市电话号码升位后为八位数，且第一位为 6 或 8 ，求随机抽取的一个电话号码为不重复的八位数的概率。

解答

记事件 A 为随机抽取的一个电话号码为不重复的八位数。
样本空间 Ω 为所有电话号码的集合，共有 $$2 \times 10^7$$ 个样本点。

有利于 A 的样本点数为 $$2 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3$$

因此，事件 A 的概率为

$$
P(A) = \frac{2 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3}{2 \times 10^7} = 0.03024
$$

几何概型

适用场景：当古典概型的试验结果为连续无穷多个时就归结为几何概型。

当随机试验的样本空间是某个区域，并且任意一点落在度量 ( 长度、面积、体积 ) 相同的子区域是等可能的，则称此随机试验为几何概型。

设几何概型的样本空间为 Ω，其度量为 m(Ω)，A 为样本空间 Ω 中的任意一个事件，其度量为 m(A)，则事件 A 出现的概率为

$$
P(A) = \frac{m(A)}{m(\Omega)}
$$

其中 m(Ω) 为样本空间 Ω 的度量，m(A) 为事件 A 的度量。

事件的运算

并集、交集、补集

$$
A \cup B = B \cup A；A \cap B = B \cap A
$$

运算律（交换律、结合律、分配律、对偶律）

结合律
$$
A \cup (B \cup C) = ( A \cup B) \cup C ;A \cap (B \cap C) = ( A \cap B) \cap C.
$$

分配律
$$
A \cup (B \cap C) = ( A \cup B) \cap ( A \cup C);A \cap (B \cup C) = ( A \cap B) \cup ( A \cap C).
$$

零律
$$
A \cup \varnothing = A;A \cap \varnothing = \varnothing.
$$

幂等律
$$
A \cup A = A;A \cap A = A.
$$

德摩根律

$$
A \cup \overline{A} = \Omega;A \cap \overline{A} = \varnothing.
$$

解释：$\Omega$ 为样本空间（也就是所有可能的结果），$\overline{A}$ 为事件 $A$ 的补集。

条件概率

适用场景：已知一个事件 $B$ 发生，求另一个事件 $A$ 发生的概率。

条件概率的定义

设 $A$ 和 $B$ 是两个事件，且 $P(B) > 0$，则在事件 $B$ 发生的条件下，事件 $A$ 发生的概率为

$$
P(A|B) = \frac{P(A \cap B)}{P(B)}
$$

我们称 $P(A|B)$ 为在 $B$ 发生的条件下 $A$ 的条件概率。

条件概率 $P(A|B)$ 满足概率公理化定义的三种性质：

非负性：$P(A|B) \geq 0$
规范性：$P(\Omega|B) = 1$
可列可加性：设 $A_1, A_2, \cdots$ 是两两互不相容的事件，则 $P(A_1 \cup A_2 \cup \cdots |B) = P(A_1|B) + P(A_2|B) + \cdots$

而在性质上，条件概率 $P(A|B)$ 与无条件概率 $P(A)$ 有如下关系：

$$
P(A) = P(A|B)P(B) + P(A|\overline{B})P(\overline{B})
$$
其中 $\overline{B}$ 是 $B$ 的补集。

条件概率的求法

利用定义求解

我们可以直接利用条件概率的定义求解，例如，设置一批产品的甲乙丙三个等级分别占 30%，50%，20%，已知每个等级的产品数量，求从这批产品中随机抽取一个产品，结果不是三等品，其为甲等级的概率。

设 $A_i$ 为第 $i$ 个等级的产品数量，已知 $P(A_1) = 0.3$，$P(A_2) = 0.5$，$P(A_3) = 0.2$，则

$$
P(A_1|\overline{A_3}) = \frac{P(A_1 \overline{A_3})}{P(\overline{A_3})} = \frac{P(A_1 \overline{A_3})}{1-P(A_3)}
$$
因为 $A_1 \overline{A_3} = A_1 - A_1 A_3$，且 $A_1 A_3 = \varnothing$，所以

$$
A_1 \overline{A_3} = A_1
$$

代入原式得

$$
P(A_1|\overline{A_3}) = \frac{P(A_1)}{1-P(A_3)} = \frac{0.3}{0.8} = 0.375
$$

利用乘法公式

我们可以利用以下乘法公式求解。

当我们设 $P(A) > 0$ 时，有 $P(AB) = P(A)P(B|A)$
或者当 $P(B) > 0$ 时，有 $P(AB) = P(B)P(A|B)$

经过推广，有

$$
P(ABC) = P(A)P(B|A)P(C|AB) \quad \text{其中} \quad P(AB) > 0
$$

条件概率例题 1

一批零件共有 100 个，其中有 10 个次品，不放回抽取 2 次，每次取一个，求第一次取到次品且第二次取到正品的概率。

解答

记事件 $A$ 为第一次取到次品，事件 $B$ 为第二次取到正品。

$$
P(AB) = P(A)P(B|A) = \frac{10}{100} \times \frac{90}{99} = 0.0909
$$

全概率公式

适用场景：已知一个事件有多种可能的原因，求该事件结果发生的概率。

若令 $A_1, A_2, \cdots, A_n$ 两两互不相容（是 $\Omega$ 的一个划分），且 $P(A_i) > 0$，则有

$$
P(B) = \sum_{i=1}^n P(B|A_i)P(A_i)
$$

全概率公式例题 1

甲口袋里有 3 个白球，2 个黑球；乙口袋里有 4 个白球，3 个黑球。现从甲口袋中任取一球放入乙口袋，再从乙口袋中任取一球。求从乙口袋中取到的球是白球的概率。

解答

这个问题体现了全概率公式的应用特征：事件 B（从乙口袋中取到白球）的发生可能由多个互斥的原因引起，我们需要考虑所有可能的情况。

完备事件组：$A_1$ 为从甲口袋中取到白球，$A_2$ 为从甲口袋中取到黑球。
这两个事件构成了一个完备事件组，即它们互斥且和为 1，这是应用全概率公式的前提条件。
事件 $B$ 为从乙口袋中取到白球。
这是我们最终要求的概率事件。

根据全概率公式，有

$$
P(B) = P(B|A_1)P(A_1) + P(B|A_2)P(A_2)
$$

这个公式体现了全概率公式的核心思想：将复杂事件 B 的概率分解为在不同条件下的概率之和。

求解

$$
P(B) = \frac{3}{5} \times \frac{5}{8} + \frac{2}{5} \times \frac{4}{8} = 0.575
$$

在这里，$\frac{3}{5}$ 和 $\frac{2}{5}$ 分别是 $P(A_1)$ 和 $P(A_2)$，
$\frac{5}{8}$ 是 $P(B|A_1)$（从甲取到白球后，乙中有 5 个白球，共 8 个球），
$\frac{4}{8}$ 是 $P(B|A_2)$（从甲取到黑球后，乙中有 4 个白球，共 8 个球）。

这种分步计算和加和的方法正是全概率公式的应用体现。

贝叶斯公式

适用场景：已知一个事件的结果，求该事件发生的原因的概率。

一项血液化验以概率 0.95 将带菌病人检出阳性，但也有 1 ％的概率误将健康人检出阳性。设已知该种疾病的发病率为 0.5 ％，求已知一个个体被此项血液化验检出阳性条件下，该个体确实患有此种疾病的概率。

这里的发病率称为先验概率，检出阳性的概率称为似然值，求得的阳性条件下患病概率称为后验概率。

后验概率的计算是贝叶斯公式的典型应用。

设 $A_1, A_2, \cdots, A_n$ 是样本空间 $\Omega$ 的一个划分（也就是互斥且各项大于零且和为 1），且 $P(A_i) > 0$，则有

$$
B = \bigcup_{i=1}^n (A_i \cap B)
$$

对于任意 $i$，有

$$
P(A_i|B) = \frac{P(A_i \cap B)}{P(B)} = \frac{P(B|A_i)P(A_i)}{\sum_{i=1}^n P(B|A_i)P(A_i)}
$$

贝叶斯公式例题 1

盒中有 6 只乒乓球，其中 4 只新球，先从中任取 2 只进行练习，用后放回盒中，接着比赛时再从盒中取 2 只，已知比赛时取出的是 2 只新球，问练习时取到几只新球的可能性大？

解答

这个问题的关键在于我们已知了结果（比赛时取出 2 只新球），而要求原因（练习时取出的新球数量）的概率。这正是贝叶斯公式的典型应用场景。

让我们定义以下事件：

$A$: 比赛时取出 2 只新球
$B_0$: 练习时取出 0 只新球
$B_1$: 练习时取出 1 只新球
$B_2$: 练习时取出 2 只新球

(1) 首先，我们使用古典概型计算各种概率：

$P(B_0) = \frac{C_2^0 \cdot C_4^2}{C_6^2} = \frac{1}{15}$
$P(B_1) = \frac{C_2^1 \cdot C_4^1}{C_6^2} = \frac{8}{15}$
$P(B_2) = \frac{C_2^2 \cdot C_4^0}{C_6^2} = \frac{6}{15}$

$P(A|B_0) = \frac{C_4^2}{C_6^2} = \frac{6}{15}$
$P(A|B_1) = \frac{C_4^2}{C_6^2} = \frac{3}{15}$
$P(A|B_2) = \frac{C_4^2}{C_6^2} = \frac{1}{15}$

(2) 使用全概率公式计算$P(A)$:

$P(A) = P(A|B_0)P(B_0) + P(A|B_1)P(B_1) + P(A|B_2)P(B_2)$
$ = (\frac{6}{15} \cdot \frac{1}{15}) + (\frac{3}{15} \cdot \frac{8}{15}) + (\frac{1}{15} \cdot \frac{6}{15})$
$ = \frac{4}{25}$

(3) 使用贝叶斯公式计算在$A$发生的条件下$B_0$、$B_1$、$B_2$发生的概率：

$P(B_0|A) = \frac{P(B_0)P(A|B_0)}{P(A)} = \frac{\frac{1}{15} \cdot \frac{6}{15}}{\frac{4}{25}} = \frac{1}{6}$
$P(B_1|A) = \frac{P(B_1)P(A|B_1)}{P(A)} = \frac{\frac{8}{15} \cdot \frac{3}{15}}{\frac{4}{25}} = \frac{4}{6}$
$P(B_2|A) = \frac{P(B_2)P(A|B_2)}{P(A)} = \frac{\frac{6}{15} \cdot \frac{1}{15}}{\frac{4}{25}} = \frac{1}{6}$

因此，练习时取到 1 只新球的可能性最大，概率为$\frac{4}{6}$。

这个问题之所以需要使用贝叶斯公式，是因为我们需要根据已知的结果（比赛时取出 2 只新球）来推断导致这个结果的原因（练习时取出的新球数量）的概率。这种从结果推因的思路正是贝叶斯公式的核心应用。通过贝叶斯公式，我们可以利用先验概率（练习时取出不同数量新球的概率）和条件概率（在不同练习情况下，比赛取出 2 只新球的概率）来计算后验概率（已知比赛结果后，推断练习情况的概率）。

事件的独立性

若 $P(AB) = P(A) \times P(B)$，则称事件 $A$ 与 $B$ 相互独立。且 $\overline{A}$ 与 $B$ 相互独立，$\overline{B}$ 与 $A$ 相互独立。甚至 $\overline{A}$ 与 $\overline{B}$ 相互独立。

证明过程这里略。如果有多个事件，必须任取任意个事件，它们都相互独立，才能说这些事件相互独立。

在实际问题中，通常利用德摩根律来将求和事件转化为求积事件来利用事件独立性。这个转换过程如下：

德摩根律（经常在离散数学中看见）

$$
\overline{A \cup B} = \overline{A} \cap \overline{B}
$$

这个转换的意义在于，如果事件 A 和 B 是独立的，那么它们的补事件 $\overline{A}$ 和 $\overline{B}$ 也是独立的。

在概率论中，交集运算与乘法运算在数学上是等价的，对于独立事件 $P(A \times B) = P(A) \times P(B)$。

因此，我们可以利用事件独立性来简化概率计算。

伯努利试验

先来看独立重复试验。

在相同条件下对试验 E 重复进行 n 次，若各次试验的结果互不影响，则称这 n 次试验是相互独立的，也称 E 是独立试验。

伯努利试验是独立试验的特例。当试验 E 只有两种结果时，称 E 为伯努利试验。将此试验独立重复 n 次，则称这一串重复试验为 n 重伯努利试验。

它的数学模型（二项概率）是：

$$
P_n(k) = C_n^k p^k (1-p)^{n-k}
$$

其中 $p$ 是单次试验成功的概率。

在实际应用中，只要记好事件 必须相互独立 ，且每次试验只有两种结果，就可以使用二项概率公式直接代数计算。

随机变量

为了量化随机试验的结果，我们引入随机变量的概念。

随机变量定义在样本空间上，定义域可以是数集。

随机变量分为离散型和连续型。离散型随机变量取值有限，连续型随机变量取值无限。如果样本空间是一个数轴，离散型随机变量取值是数轴上的有限个点，连续型随机变量取值是数轴上的一个区间。

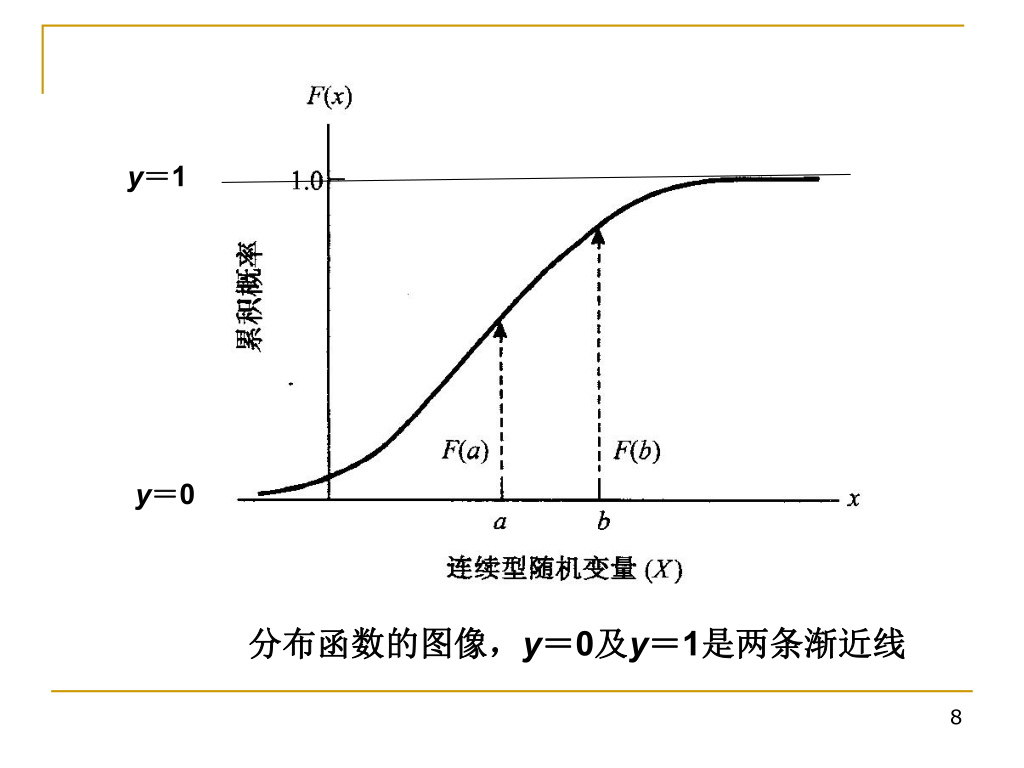
以下是连续型随机变量的图像：

设一口袋内含有 -1,2,2,2,3,4 六个球，从中任取一球，记随机变量 $X$ 为取到球的数字，则 $X$ 的取值为 -1,2,3,4。

分布律（一般是表格）如下

$X$	-1	2	3	4
$P$	1/6	3/6	1/6	1/6

则其分布函数为

$$
F(x) = \begin{cases}
0, & x < -1 \\
\frac{1}{6}, & -1 \leq x < 2 \\
\frac{2}{3}, & 2 \leq x < 3 \\
\frac{5}{6}, & 3 \leq x < 4 \\
1, & 4 \leq x
\end{cases}
$$